Time

Time in Physics

Our universe is described using a notion of spacetime, in which events take place. These events are characterised by their spatial coordinates, as well as “location” in time, so spacetime is a special type of Metric space where one coordinate is time. The time coordinate is very special, as it is the only coordinate with which it is meaningful to define an ordering in the values given, the order of time[1]. The arrow of time defines a partial order of all spacetime events. Any physical law that describes natural events has to also be sequential: one event causes a subsequent event if its time variable is lower and not otherwise[1].

Newton conceptualised “absolute time”, which assumes that time flows at the same rate for all observers in the Universe:

Absolute, true, and mathematical time, in and of itself and of its own nature, without reference to anything external, flows uniformly and by another name is called duration.

Albert Einstein changed the notion of time for us, by formulating the special theory of relativity that states: time flows at different rates for different observers. Hermann Minkowski (who was actually born close to what is now Kaunas, so, naturally, he is my favourite scientist) formally united the parameters of time and space, giving rise to the notion of a fundamental four-dimensional entity, spacetime. Citing Minkowski:

Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.

If we consider that time is empirically related to change, which is a variation or sequence of occurrences, then, intuitively, the latter provides us with a notion of something that flows, and thus the emergent character of time (Lobo,2008). We can observe events as points in space at instances of time. A sequence of events has a determined temporal order, which is experimentally verified as specific events – effects – are triggered off by others – causes – thus providing us with the notion of causality.

An important aspect of the nature of time is its arrow. Universe is governed by dynamical laws of physics which state that given the initial conditions of a physical state, these laws determine the evolution of the system over time. Many equations of dynamics are symmetric under time reversal, however. For example suppose a system with variables ($\mathbf{q},\mathbf{p}$), where $\mathbf{q}$ is a vector of positions of the system and $\mathbf{p}$ describes its momentum. Hamiltonian $H(\mathbf{q},\mathbf{p})$ defines the motion of the system via equations of motion: $\frac{d\mathbf{q}}{d t} = \frac{\partial H}{\partial \mathbf{p}} \qquad \frac{d\mathbf{p}}{d t} = -\frac{\partial H}{\partial \mathbf{q}}.$
Since hamiltonian is symmetric: $H(\mathbf{q},\mathbf{p})=H(\mathbf{q},-\mathbf{p})$, it leads to invariance of equations of motion under transformation of $(\mathbf{q},\mathbf{p},t)\rightarrow (\mathbf{q},\mathbf{-p},-t)$.

Despite the time-reversal symmetry property of equations of motion, thermodynamics, general relativity, and quantum mechanics raise issues about the absence of the time arrow. For instance, the Second Law of Thermodynamics, which states that in an isolated system the entropy (which is a measure of disorder) increases provides a thermodynamic arrow of time, shaking the time-irreversibility and opening doors to causality. For example, consider a macroscopic number of gas molecules in one of the two compartments of a tank. When the connection between two compartments is opened up, we see that the molecules distribute across two compartments evenly. If one watches a film of this gas flow in reverse, one sees the opposite: particles, distributed evenly across two compartments flow towards a state in which all particles are in one compartment. Although theoretically possible , statistically such state is highly improbable. Such time irreversibility in thermodynamic systems is encapsulated in Boltzmann’s second law of thermodynamics: entropy is monotonically increasing function of time. Notably, Maxwell proposed a thought experiment, which supposedly violates the second law of thermodynamics. In the experiment Maxwell’s daemon opens and closes frictionless doors between two compartments, only allowing a particle of type A to flow from compartment 1 to 2, and particle of type B only allowing to flow from compartment 2 to 1, thereby decreasing entropy.

Newtonian physics operates in a setting where space and time are separate entities. It is with conjunction of the principle of Galilean Relativity that states: dynamical laws of physics are the same when referred to any uniformly moving frame. Such frames are called inertial. Importantly, the Galilean transformations state that an event in one inertial frame is related to another inertial frame where the transformation of its temporal coordinate is $t’\rightarrow t$. As spatial coordinates and temporal coordinates of some two points are independently invariant under Galilean transformations, in Newtonian dynamics time and space are separate entities.

Oftentimes, we use a metric to define distances between points. Given $dx^{\mu }$ a $\mu^{\textrm{th}}$ component of an infinitesimal coordinate displacement vector, the metric determines the invariant square of an infinitesimal line element, often referred to as an interval, for two events in the same inertial frame, defined as $ds^2 = \sum_{\mu,\nu=0}^Dg_{\mu\nu}dx^{\mu}dx^{\nu},$ where $g_{\mu\nu}$ is called a metric, which is an operator, characteristic of a space that it describes. For instance, in three-dimensional Euclidean space where $g_{\mu\nu}$ is the identity matrix, $ds^2 = g_{xx}dx^xdx^x+g_{yy}dx^ydx^y+g_{zz}dx^zdx^z=(dx)^2+(dy)^2+(dz)^2$.

Although capable of describing the motion of familiar objects such as balls and feathers, time invariance and universal time were incompatible with Maxwell’s equations of electromagnetism which describe how fluctuating electric and magnetic fields propagate at a constant speed ($c$) in a vacuum.

The two entities of space and time were joined together by Einstein, who dropped the postulate of absolute time and in the special theory of relativity, postulated:

• The speed of light, c, is the same in all inertial frames
• Principle of relativity: the laws of physics take the same form in every inertial frame.

Instead of Galilean transformations, Einstein used Lorentz transformations, in which time and space coordinates are mixed, as $t’\rightarrow \gamma (t-vx/c^2)$ where $\gamma$ is a scalar. Maxwell’s equations are invariant under Lorentz transformations.

An interval between two events in a spacetime in the same inertial frame are defined using Minkowski metric $g=(-c^2,1,1,1)$, giving $ds^2 = (cdt)^2-dx^2-dy^2-dz^2,$ This definition of an interval is invariant under Lorentz transformations, and as both space and time form a connected 4-d entity, it can be considered as an underlying geometrical property of spacetime itself. The sign of the interval is also invariantly defined:

• time-like: $ds^2<0$,
• space-like: $ds^2>0$,
• light-like: $ds^2=0$.

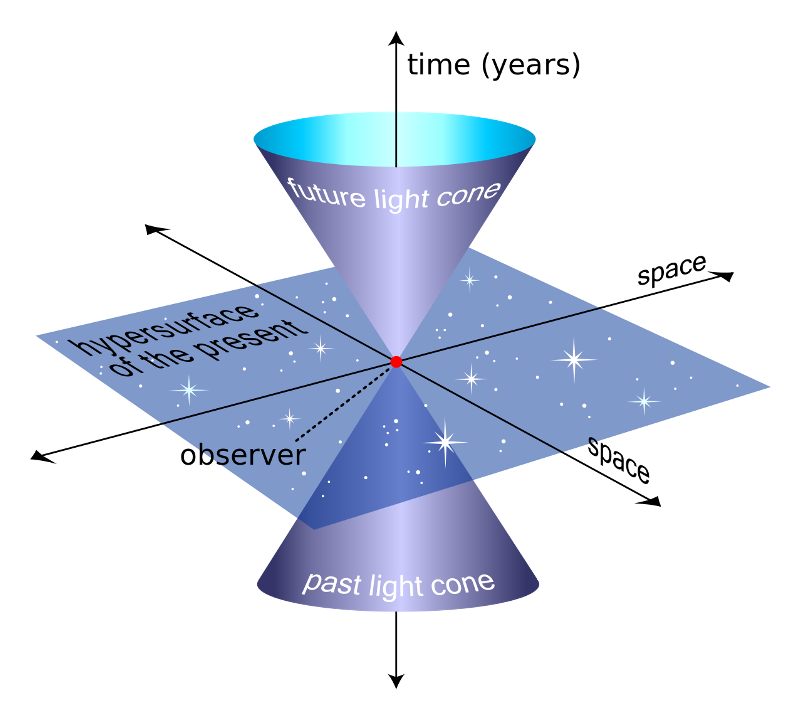For each point $v$, we can identify regions of influence, namely future and past events. For a spacetime event $v$, points for which $ds^2<0$ holds are those, which travel at a velocity $v<c$ and they are also within cones that have an angle X. Observers moving with a relative velocity $v < c$ travel along timelike curves, for instance as depicted by the curve in Fig. 2, which is denoted by the worldline of the observer. Now, there is a unique time measured along a worldline, denoted as proper time. A signal sent from v to u will be able to reach u, thus v is causally connected to u. The exterior of the lightcones is elsewhere - v cannot influence the yellow spacetime events, nor they can influence v. Thus time-like-separated events are said to be causal, space-like-separated events are acausal.

Physical causality

Let us, finally, define what we mean by causality in a physical sense. In both Einstein’s theory of special and general relativity, physical causality means that an effect cannot occur from a cause that is not in the back (past) light cone of that event. Similarly, a cause cannot have an effect outside its front (future) light cone. These restrictions are consistent with the constraint that mass and energy that act as causal influences cannot travel faster than the speed of light and/or backwards in time. In quantum field theory, observables of events with a spacelike relationship, “elsewhere”, have to commute, so the order of observations or measurements of such observables do not impact each other. The word causality in this context means that all effects must have specific physical causes due to fundamental interactions.

It is possible to show that evidence for the local arrow of time accumulates from the behavior of individual degrees of freedom and their interactions.

References

[1] G t Hooft Frontiers in Physics and 2018. Time, the arrow of time, and Quantum Mechanics.

[2] Isaac Newton. The Principia: mathematical principles of natural philosophy.